Elipse
Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución.Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.

Historia
La elipse, como curva geométrica, fue estudiada por Menecmo, investigada por Euclides, y su nombre se atribuye a Apolonio de Perge. El foco y la directriz de la sección cónica de una elipse fueron estudiadas por Pappus. En 1602, Kepler creía que la órbita de Marte era ovalada, aunque más tarde descubrió que se trataba de una elipse con el Sol en un foco. De hecho, Kepler introdujo la palabra «focus» y publicó su descubrimiento en 1609. Halley, en 1705, demostró que el cometa que ahora lleva su nombre trazaba una órbita elíptica alrededor del Sol.Elementos de una elipse
La elipse es una curva plana y cerrada, simétrica respecto a dos ejes perpendiculares entre sí:
- El semieje mayor (el segmento C-a de la figura), y
- el semieje menor (el segmento C-b de la figura).
Miden la mitad del eje mayor y menor respectivamente.
mieje menor
De la definición de elipse, el extremo del eje menor equidista de los focos y dichas distancias (F1-C y F2-C) equivalen a la medida delsemieje mayor a.
El centro de la elipse, el foco y el extremo del semieje menor conforman un triángulo rectángulo. Aplicando el Teorema de Pitágoras:
donde (ℓ) es el semi-latus rectum de una elipse.
Parámetros de una elipse. El semieje menor: b
Semieje mayor
En matemáticas, el semieje mayor de una elipse es la mitad del diámetro más largo; su símbolo es a. En astronomía, es equivalente a la distancia media de un objeto que órbita alrededor de otro, ya que el objeto central (por ejemplo, el Sol) ocupa uno de los focos.Puntos de una elipse
Los focos de la elipse son dos puntos equidistantes del centro, F1 y F2 en el eje mayor. La suma de las distancias desde cualquier punto P de la elipse a los dos focos es constante, e igual a la longitud del diámetro mayor, (PF1 + PF2 = 2a).
Si F1 y F2 son dos puntos de un plano, y 2a es una constante mayor que la distancia F1F2, un punto Ppertenecerá a la elipse si se cumple la relación:
donde  es la medida del semieje mayor de la elipse.
es la medida del semieje mayor de la elipse.
 es la medida del semieje mayor de la elipse.
es la medida del semieje mayor de la elipse.Ejes de una elipse
El eje mayor 2a, es la mayor distancia entre dos puntos adversos de la elipse. El resultado constante de la suma de las distancias de cualquier punto a los focos equivale al eje mayor. El eje menor 2b, es la menor distancia entre dos puntos adversos de la elipse. Los ejes de la elipse son perpendiculares entre si.
Excentricidad de una elipse
La excentricidad ε (épsilon) de una elipse es la razón entre su semidistancia focal (segmento que va del centro de la elipse a uno de sus focos), denominada por la letra c, y su semieje mayor. Su valor se encuentra entre cero y uno.
Parámetros de una elipse. El semieje mayor está representado aquí por a
 , con
, con 
Dado que 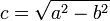 , también vale la relación:
, también vale la relación:
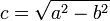 , también vale la relación:
, también vale la relación:
o el sistema:
La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero.3 La designación tradicional de la excentricidad es la letra griega ε llamada épsilon.
(No se debe usar la letra e para designarla, porque se reserva para la base de los logaritmos naturales o neperianos. Véase: número e).
Excentricidad angular de una elipse
La excentricidad angular  es el ángulo para el cual el valor de la función trigonométrica seno concuerda con la excentricidad
es el ángulo para el cual el valor de la función trigonométrica seno concuerda con la excentricidad  , esto es:
, esto es:
 es el ángulo para el cual el valor de la función trigonométrica seno concuerda con la excentricidad
es el ángulo para el cual el valor de la función trigonométrica seno concuerda con la excentricidad  , esto es:
, esto es:Constante de la elipse
En la figura de la derecha se muestran los dos radio vectores correspondientes a cada punto P de una elipse, los vectores que van de los focos F1 y F2 a P. Las longitudes de los segmentos correspondientes a cada uno son PF1 (color azul) y PF2 (color rojo), y en la animación se ilustra como varían para diversos puntos P de la elipse.
Como establece la definición inicial de la elipse como lugar geométrico, para todos los puntos P de la elipse la suma de las longitudes de sus dos radio vectores es una una cantidad constante igual a la longitud 2a del eje mayor:
- PF1 + PF2 = 2a
En la elipse de la imagen 2a vale 10 y se ilustra, para un conjunto selecto de puntos, cómo se cumple la definición.
Directrices de la elipse
Cada foco F de la elipse está asociado con una recta paralela al semieje menor llamada directriz (ver ilustración de la derecha). La distancia de cualquier punto P de la elipse hasta el foco F es una fracción constante de la distancia perpendicular de ese punto P a la directriz que resulta en la igualdad:
La relación entre estas dos distancias es la excentricidad  de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
 de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
|
Además de la bien conocida relación  , también es cierto que
, también es cierto que  , también es útil la fórmula
, también es útil la fórmula  .
.
 , también es cierto que
, también es cierto que  , también es útil la fórmula
, también es útil la fórmula  .
.
Aunque en la figura solo se dibujó la directriz del foco derecho, existe otra directriz para el foco izquierdo cuya distancia del centro O es -d, la cual además es paralela a la directriz anterior.
Ecuaciones de la elipse
En coordenadas cartesianas
Forma cartesiana centrada en origen
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
donde a > 0 y b > 0 son los semiejes de la elipse, donde si a corresponde al eje de las abscisas y b al eje de las ordenadas la elipse es horizontal, si es al revés, entonces es vertical. El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2ea, siendo e la excentricidad y a el semieje mayor.
Forma cartesiana centrada fuera del origen
Si el centro de la elipse se encuentra en el punto (h,k), la ecuación es:
En coordenadas polares
Forma polar centrada en origen
En coordenadas polares, con origen en su centro, la ecuación de la elipse es:
(epc 1)
Una ecuación más elegante que la anterior (pero que obliga a pre-calcular la excentricidad  ), es:
), es:
 ), es:
), es:(epc 2)
Para ambas ecuaciones a es el semieje mayor, b es el semieje menor de la elipse, θ es el ángulo polar y para la () ε es la excentricidad.
Si no se quiere pre-calcular la excentricidad  convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
 convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().Formas polares centradas en un foco
En coordenadas polares, con el origen en uno de sus focos, la ecuación de la elipse es:
(501)
Para el otro foco:
(502)
En el caso un poco más general de una elipse con un foco en el origen y el otro foco en la coordenada angular 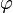 , la forma polar es:
, la forma polar es:
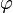 , la forma polar es:
, la forma polar es:(503)}
El ángulo 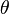 de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas
de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas  es el llamado semi-latus rectum de la elipse, normalmente denotado
es el llamado semi-latus rectum de la elipse, normalmente denotado  . El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.
. El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.
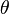 de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas
de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas  es el llamado semi-latus rectum de la elipse, normalmente denotado
es el llamado semi-latus rectum de la elipse, normalmente denotado  . El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.
. El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.Formas paramétricas
con 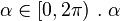 no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre  y θ es
y θ es
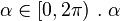 no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre  y θ es
y θ es-
 .
.
La ecuación paramétrica de una elipse con centro en  en la que el parámetro
en la que el parámetro 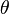 sea concordante con el ángulo polar respecto al centro desplazado
sea concordante con el ángulo polar respecto al centro desplazado  es:
es:
 en la que el parámetro
en la que el parámetro 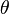 sea concordante con el ángulo polar respecto al centro desplazado
sea concordante con el ángulo polar respecto al centro desplazado  es:
es:
con  . El parámetro
. El parámetro 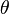 es el ángulo de un sistema polar cuyo origen está centrado en
es el ángulo de un sistema polar cuyo origen está centrado en  .
.
 . El parámetro
. El parámetro 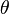 es el ángulo de un sistema polar cuyo origen está centrado en
es el ángulo de un sistema polar cuyo origen está centrado en  .
.Área interior de una elipse
El área de la superficie interior de una elipse es:
Siendo a y b los semiejes.4
Longitud de una elipse
El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de segunda especie.
Sin embargo, el matemático Ramanujan ideó una ecuación más simple que se aproxima razonablemente a la longitud de la elipse, pero en grado menor que la obtenida mediante integrales elípticas. Ramanujan, en su fórmula, entre otros valores utiliza el “semieje mayor” y el “semieje menor”. Ecuación de la longitud de una elipse:
Propiedades notables
La elipse goza de ciertas propiedades asociadas a sus componentes, como se puede ver en Analogía de Michelson y Morley.
La elipse como cónica
La elipse surge de la intersección de una superficie cónica con un plano, de tal manera que la inclinación del plano no supere la inclinación de la recta generatriz del cono, consiguiendo así que la intersección sea una curva cerrada. En otro caso el corte podría ser una hipérbola o una parábola. Es por ello que a todas estas figuras bidimensionales se las llamasecciones cónicas o simplemente cónicas.
La elipse como hipotrocoide
La elipse es un caso particular de hipotrocoide, donde R = 2r, siendo R el radio de la circunferencia directriz, y r el radio de la circunferencia generatriz.
En una curva hipotrocoide, la circunferencia que contiene al punto generatriz, gira tangencialmente por el interior de la circunferencia directriz.
Construcción paramétrica de una elipse
Se dibujan dos circunferencias concéntricas cuyos diámetros equivalen a la medida de los ejes ortogonales de la futura elipse. Si trazamos segmentos palalelos a los ejes principales Xe Y, partiendo del extremo de los radios alineados, la intersección de dichos segmentos son puntos de la elipse.
Anamorfosis de una circunferencia en una elipse
Determinada trasformación de la circunferencia (al deformar ortogonalmente el plano cartesiano asociado a ella), se denomina anamorfosis. Se corresponde con una perspectiva especial. El término anamorfosis proviene del idioma griego y significa trasformar.
En el caso de la circunferencia, si el plano cartesiano se divide en cuadrados, cuando dicho plano se «deforma» en sentido del eje X, el Y, o ambos, la circunferencia se transforma en una elipse y los cuadrados en rectángulos.
Elipses semejantes
Se dice que dos figuras son semejantes cuando se diferencian sólo en el tamaño (pero no en la forma), de tal manera que multiplicando todas las longitudes por un factor dado, se pasa de una figura a la otra. Hay un teorema de utilidad en Física5 acerca de la intersección de una recta con dos elipses semejantes y concéntricas.
|
Explicación: El teorema es cierto, por simetría, en el caso particular en que las elipses dadas sean dos circunferencias concéntricas. Contrayendo o dilatando uniformemente una de las direcciones coordenadas, mediante anamorfosis, podemos transformar cualquier caso en este caso particular, pues todos los segmentos con la misma pendiente cambian su longitud en la misma proporción. Por tanto, puesto que al final del proceso los dos segmentos de la recta tienen la misma longitud, la tenían ya al principio.
No deben confundirse las elipses semejantes con las elipses cofocales.
La elipse en mecánica celeste
En mecánica celeste clásica, dos masas puntuales sometidas exclusivamente a interacción gravitatoria describen una órbita elíptica (o circular 6 ) la una en torno a la otra cuando la órbita es cerrada. Un observador situado en cualquiera de las masas verá que la otra describe una elipse uno de cuyos focos (o centro) está ocupado por el propio observador. La excentricidad y otros parámetros de la trayectoria dependen, para dos masas dadas, de las posiciones y velocidades relativas. Los planetas y el Sol satisfacen la condición de masas puntuales con gran precisión porque sus dimensiones son mucho más pequeñas que las distancias entre ellos. Lacinemática de la órbita se rige por las leyes de Kepler.
En la figura pueden verse dos intervalos de tiempo distintos de una órbita elíptica que cumplen la segunda ley de Kepler: "en tiempos iguales una masa en órbita barre con su radio vector áreas iguales". Cuando el "planeta" está más cerca de la "estrella" va más rápido y cuando está lejos va más despacio, pero de tal manera que su velocidad areolar es la misma en ambos casos. Esto significa que las áreas de los sectores elípticos amarillos son iguales y sus arcos t0 t1 se han recorrido en intervalos de tiempo iguales, Δt = t1 - t0. La "estrella" está situada en P, uno de los focos de la elipse.
Hipérbola
Etimología. Hipérbole e hipérbola
Hipérbola deriva de la palabra griega ὑπερβολή (exceso), y es cognado de hipérbole (la figura literaria que equivale a exageración).
Véase también: hipérbole
[editar]Historia
Según la tradición, las secciones cónicas fueron descubiertas por Menecmo, en su estudio del problema de la duplicación del cubo,2 donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Procloy Eratóstenes.3
Sin embargo, el primero en usar el término hipérbola fue Apolonio de Perge en su tratado Cónicas,4 considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.
[editar]Ecuaciones de la hipérbola
Ecuaciones en coordenadas cartesianas: Ecuación de una hipérbola con centro en el origen de coordenadas
 y ecuación de la hipérbola en su forma canónica. y ecuación de la hipérbola en su forma canónica.
Ecuación de una hipérbola con centro en el punto

Ejemplos:
a)
b)
Si el semieje transverso a se encuentra en el eje x, y el semieje conjugado b, en el eje y, entonces la hipérbola es horizontal; si es al revés, es vertical. La excentricidad de una hipérbola siempre es mayor que uno.
Ecuación de la hipérbola en su forma compleja
Una hipérbola en el plano complejo es el lugar geométrico formado por un conjunto de puntos
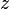 , en el plano , en el plano 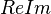 ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias  , a dos puntos fijos llamados focos , a dos puntos fijos llamados focos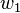 y y  , es una constante positiva igual al doble de la distancia (o sea , es una constante positiva igual al doble de la distancia (o sea  ) que existe entre su centro y cualesquiera de sus vértices del eje focal. ) que existe entre su centro y cualesquiera de sus vértices del eje focal.
La ecuación queda:

Evidentemente esta operación se lleva a cabo en el conjunto de los números complejos.
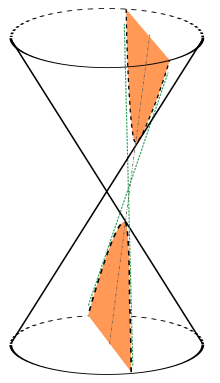
[]Ecuaciones en coordenadas polaresHipérbola abierta de arriba a abajo:
Hipérbola abierta de noroeste a sureste:
Ecuaciones paramétricas
Hipérbola abierta de derecha a izquierda:
Hipérbola abierta de arriba a abajo:
|



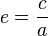 , su relación será:
, su relación será:
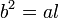







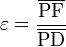

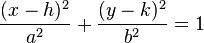

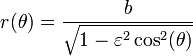

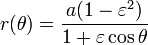


 el semieje mayor y
el semieje mayor y  el menor, es:
el menor, es:


![P \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,](http://upload.wikimedia.org/wikipedia/es/math/d/3/4/d34a512a10d8825e517cf922f7fca13c.png)













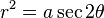



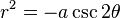



No hay comentarios:
Publicar un comentario